ABSTRACCIÓN, ABSTRACTOABSTRACCIÓN, ABSTRACTO El verbo
griego Tanto Similarmente, el verbo latino abstraho (abstrahere) se usó en varios contextos para designar las operaciones de separar, destacar, arrancar del, alejarse de, renunciar a, sustraer, etcétera. Ejemplos de tales usos son: abstrahere.... e sinu patriae = arrancar a alguien de su tierra natal; abstrahere.... de conspectu matris = arrancar a alguien del seno de su madre; senectus a rebus gerendis abstrahit = la senectud (los viejos) se retira de los asuntos públicos; omnia in duas partes abstracta sunt = el Estado (literalmente: los todos) se había dividido en dos campos; animus a se corpore abstrahit = el alma se halla separada del cuerpo. Los términos 'abstraer' y 'abstracción' (o los correspondientes vocablos griegos y latinos) fueron usados por filósofos antiguos y medievales en sentidos varios, aunque de alguna manera análogos, pero especialmente desde Aristóteles tales términos comenzaron a adquirir, junto a sus usos más corrientes, ciertos significados «técnicos» o «especializados». Éstos son los que se han concretado en la noción de abstracción como la acción y efecto de separar conceptualmente algo de algo, esto es, de poner algo (alguna característica o propiedad, sobre todo) mentalmente aparte. Cabe poner aparte en este sentido una característica o una propiedad de un objeto —por ejemplo, tal determinado color o tal determinada forma, de tal o cual determinado objeto—, con el fin de considerar esta característica o propiedad «separadamente»; pero cabe asimismo poner aparte lo que se estima que es una característica o propiedad común a varios objetos —por ejemplo, el color azul de varios objetos azules— y considerar entonces lo que se pone aparte como algo «general» o «universal». Cabe asimismo poner aparte ciertos «objetos» —por ejemplo, el círculo o el triángulo, considerados «separadamente» de los objetos circulares o triangulares, o de posibles objetos circulares o triangulares (cabe «poner aparte» un miriágono, aunque no haya ningún objeto de mil lados). El verbo Si consideramos que, según Platón, hay en las ideas, metafísicamente hablando, «más» que en las cosas, de suerte que tales ideas, lejos de ser una «disminución» de la realidad (como ocurre cuando se tiene mentalmente la idea de una silla más bien que la propia silla), son una «potenciación» de la realidad; y si, además, suponemos que las ideas se obtienen mediante «abstracción», habrá que concluir que para Platón lo «abstracto», en tanto que «universal», es más real que lo particular y singular. Puede hablarse entonces, como se ha hecho a menudo, de un «realismo de la abstracción». Pero esto es un anacronismo, ya que Platón no entendía por 'abstraer' y 'abstracción' (es decir, por los correspondientes vocablos griegos) lo mismo que se ha entendido luego. Si se aplica el posterior sentido de 'abstraer' y 'abstracción' a Platón se puede concluir que este autor tuvo una determinada concepción de la abstracción. Es la que se ha calificado a veces de «abstracción metafísica». No hay inconveniente en cometer este anacronismo siempre que se tenga conciencia de él. Pero se es más fiel a las intenciones y al lenguaje de Platón cuando, en vez de hablar de «abstraer», «abstracción» y «abstracto», se habla de «separar», «separación» y «separado» en el sentido en que hemos tratado de la noción de separación (VÉASE). Aristóteles, que usó también los términos Las doctrinas aristotélicas de la abstracción pasaron a parte de la filosofía medieval principalmente por los comentarios de Boecio al Isagoge de Porfirio. Muchos autores hasta el siglo XIII siguieron la tesis de que la mente puede abstraer «formas» de las cosas sin que ello quiera decir que estas «formas» están realmente separadas de las cosas: esta tesis podría llamarse «conceptualismo de la abstracción» y ejerció influencia sobre casi todos los filósofos que mantuvieron alguna posición intermedia entre el realismo y el nominalismo en la doctrina de los universales (VÉASE). En todo caso, numerosos filósofos medievales usaron la noción de abstracción en su explicación del origen y estructura del conocimiento. Otros filósofos, acaso tan numerosos como los anteriores, no se ocuparon, en cambio, de cuestiones relativas a la abstracción. Ello sucedió especialmente con los pensadores que seguían más fielmente la tradición agustiniana y para los cuales, como para San Agustín, el alma es «iluminada» por Dios (véase ILUMINACIÓN) de modo que, al poseer las Formas, no necesita sacarlas mediante abstracción de las cosas. El debate entre los que podrían llamarse «abstraccionistas» y los que se podrían calificar de «iluministas» tuvo lugar asimismo, aunque en formas muy distintas, en la filosofía árabe. En ésta, más aún que en la medieval cristiana, se hicieron esfuerzos para conciliar la tradición neoplatónica —que es una de las raíces intelectuales del agustinismo—con la aristotélica. Testimonio al respecto es Avicena, que influyó, además, sobre filósofos escolásticos cristianos. Avicena estimó que hay diversos grados de abstracción a partir de la abstracción sensible, pero que, a la vez, la mente individual humana recibe las emanaciones de las Formas inmateriales en el proceso de la actividad «intelectiva». Esta concepción de la mente humana individual se funda en parte en la idea de una doble orientación de la misma hacia las cosas sensibles y hacia las Formas inteligibles; esta «doble orientación» constituye una de las características del pensamiento de varios autores cristianos, como Mateo de Aquasparta. Por otro lado, los nominalistas se opusieron a la tesis de que lo «abstraído», aun si es meramente «conceptual», es «universal»; lo «abstraído» es siempre singular aun cuando pueda servir para comparaciones con otras «entidades abstraídas» similares. Guillermo de Occam insistió en que no puede pensarse separadamente (por abstracción) lo que no existe separadamente (abstraído). Ello no quiere decir que sea imposible pensar una cualidad de un objeto independientemente de otra cualidad del mismo objeto. A diferencia de los «iluministas» en sentido más estricto, los nominalistas no desecharon hacer uso de la noción de abstracción. Así, por ejemplo, Occam manifiesta que hay una abstracción que consiste en aprehender una cosa sin aprehender la otra (la blancura de la leche sin su sabor; cfr. supra); una abstracción mediante la cual se separa de lo singular un concepto universal (bien que no existente de por sí); y una abstracción mediante la cual se afirma un predicable de un sujeto sin afirmar otro predicable igualmente admisible como atributo (como ocurre en la abstracción matemática) (Exp. super Physicam, fol. 111; II Sent. q. 14 y 15, cit. en Léon Baudry, Lexique philosophique de Guillaume d'Occam, 1957, s. v. «Abstractio», pág. 6). El primer y tercer tipo de abstracción son los que parecen interesar más, si no exclusivamente, a muchos autores nominalistas. En algunos textos escolásticos se encuentra una distinción entre el acto de conocimiento absoluto y el comparativo. El acto absoluto es una abstracción mediante la cual se conoce la cosa misma «absolutamente» («separadamente»), es decir, la cosa misma abstraída de toda relación con otra cosa (donde 'cosa' puede ser 'propiedad'). Este acto es estimado a veces negativo por cuanto se desatienden ciertos rasgos de la cosa sometida a abstracción, pero es estimado positivo por cuanto se atiende a los rasgos abstraídos. Cuando en el acto positivo de la abstracción se hace presente la naturaleza, o forma, del objeto considerado, la abstracción es de carácter intelectual. A su vez, esta abstracción intelectual puede ser de primera intención, cuando se obtiene un concepto universal o esencia; y de segunda intención, cuando se obtiene un concepto trascendental (VÉASE). La abstracción de segunda intención se funda en la de primera intención. Santo Tomás (S. theol. I, q. XL, a 3) habla de dos clases de abstracción: 1) La abstracción por medio de la cual se separa lo general de lo particular. Ejemplo: animal se separa de hombre. Esta abstracción «destruye» los objetos separados, como ocurre cuando se separa del hombre su racionalidad. 2) La abstracción por medio de la cual se separa la forma de la materia. Ejemplo: círculo se separa de todo cuerpo sensible circular. Esta abstracción no «destruye» ninguno de los dos objetos sobre los cuales opera, como ocurre cuando se separa círculo de materia circular y se conservan ambas ideas. Con respecto a Dios, aunque se separan las propiedades no personales, el espíritu sigue conservando la idea de hipóstasis. Santo Tomás habla asimismo (S. theol. I, q. LXXXV, a 1 ad 1) de la división de la abstracción en abstracción por medio de composición y por medio de división. Fundándose en Santo Tomás, especialmente en S. theol. I, q. XL, art. 3, obj., Cayetano (Comm. in De ente et essentia, proemium, q. 1) y Juan de Santo Tomás (Cursus philosophicus. Logica, Pars 2, q. 27, art. 1) propusieron una doctrina relativa a varias clases y grados de abstracción que ha sido aceptada por muchos autores escolásticos y neoescolásticos y ha sido popularizada por Jacques Maritain (Distinguer pour unir ou les degrés du savoir, nueva ed. 1932, Parte I, cap. 2, págs. 71 y sigs.). Juan de Santo Tomás comienza por distinguir entre la abstracción extensiva o abstracción de totalidades universales (abstracción total, abstractio totalis) y la abstracción formal o abstracción de tipos inteligibles (abstractio formalis). La abstracción total «separa un objeto de los inferiores de que es predicable; esta clase de abstracción es una condición general para las ciencias, puesto que éstas no se ocupan de individuos, sino de universales»; así, la abstracción total es «abstracción o extracción del todo universal por la cual sacamos `hombre' de 'Pedro' y de 'Pablo', 'animal' de 'hombre', etc., pasando así a universales cada vez más vastos» (Maritain, op. cit., pág. 71). La abstracción formal —que, según Juan de Santo Tomás, no es un acto del intelecto, ni una denominación intrínseca resultante de tal acto, su no «abstractibilidad objetiva»— es «la que separa aspectos formales de lo que es material o potencial, constituyendo o fundando de ese modo la inteligibilidad» (loc. cit.). Maritain precisa que mediante esta abstracción «separamos de los datos contingentes y materiales lo que pertenece a la razón formal o a la esencia de un objeto del saber» (op. cit., pág. 72). De acuerdo con Juan de Santo Tomás, el objeto de conocimiento se hace inteligible en diversos modos según se halle más o menos separado de la materia y de las condiciones materiales (en los sentidos aristotélicos de 'materia' y 'material'). Como las diferencias entre las ciencias son función del grado de abstracción formal propio de cada una, hay que considerar varios grados de abstracción formal. Seguimos la exposición de Maritain al respecto. 1) Primer grado de abstracción, propio de la Physica, la cual, según Juan de Santo Tomás, «abstrae meramente de la materia singular y considera el mundo sensible». Maritain pone de relieve que mediante este grado de abstracción «el espíritu puede considerar objetos abstraídos y purificados sólo de la materia en tanto que funda la diversidad de los individuos en el seno de la especie, en tanto que es principio de individuación; ... el espíritu considera entonces los cuerpos en su realidad móvil y sensible, los cuerpos revestidos de sus cualidades y propiedades experimentalmente comprobables; tal objeto no puede ni existir sin la materia y las cualidades ligadas a ella, ni ser concebido sin ella» (Degrés, pág. 71). 2) Segundo grado de abstracción, propio de la Mathematica, la cual, según Juan de Santo Tomás, «abstrae, además, de la materia sensible, y considera la cantidad». Para Maritain, «el espíritu puede considerar objetos abstraídos y purificados de la materia en tanto que funda, en general, las propiedades sensibles, activas y pasivas, de los cuerpos; entonces considera únicamente una cierta propiedad que separa de los cuerpos ... la cantidad, nombre o extensión en sí: objeto del pensamiento que no puede existir sin la materia sensible, pero que puede ser concebido sin ella» (op. cit., págs. 71-72). 3) Tercer grado de abstracción, propio de la Metaphysica, la cual, según Juan de Santo Tomás, «abstrae inclusive de la materia inteligible y considera la substancia o el ser». Para Maritain, este grado de abstracción tiene lugar cuando el espíritu considera «objetos abstraídos y purificados de toda materia, sin retener en las cosas más que el propio ser en ellas embebido, el ser tal como tal y sus leyes: objetos de pensamiento que no sólo pueden ser concebidos sin la materia, sino que pueden inclusive existir sin ella, sea que no existan jamás en la materia, cual Dios y los espíritus puros, sea que existan tanto en las cosas materiales como en las inmateriales, cual la substancia, la cualidad, el acto y la potencia, la belleza, la bondad, etc.» (op. cit., págs. 73-74). Las anteriores doctrinas no aspiran a resolver todos los puntos en litigio. Así, Juan de Santo Tomás reconoce que cada uno de los tres géneros de ciencia contiene diversas especies de ciencia, no siendo fácil «mostrar cómo la abstracción da cuenta de la diversidad específica de las ciencias». Maritain trata de afrontar la cuestión de la complejidad de la Physica distinguiendo entre dos clases de ciencias: ciencias de constatación, especialmente inductivas, o ciencias empíricas de la Naturaleza sensible, y una ciencia del ser corporal explicativa, o filosofía de la Naturaleza sensible. Reconoce asimismo que no es fácil (aunque estima que no imposible) dar cuenta de la estructura de la ciencia físico-matemática moderna en función de los grados de abstracción (op. cit., págs. 80 y sigs.). De todos modos, los autores escolásticos que han adoptado las doctrinas reseñadas, y en particular Maritain, han alegado que la distinción entre abstracción total y formal es necesaria para evitar los «errores» en que han caído casi todos los autores modernos (empiristas, nominalistas, positivistas, etc.), por no haber tenido en cuenta tal distinción y por haber tendido a considerar exclusivamente el aspecto «total» de la abstracción. Ello les ha impedido reconocer el carácter peculiar de la abstracción total y les ha llevado casi siempre a negar la posibilidad de una abstractio formalis metaphysica. Los filósofos modernos a que alude Maritain son legión, pero difieren entre sí mucho más de lo que dicho autor sugiere. Pueden encontrarse referencias a la abstracción o al uso de procedimientos abstractivos en Descartes; tal sucede cuando indica que se pueden tener nociones distintas de la extensión y del pensamiento como constituyendo la naturaleza de los cuerpos y del alma respectivamente (Princ. I, 63). Cartesianamente, los autores de la Logique de Port-Royal señalan que «puede considerarse un modo sin hacer una reflexión distinta sobre la substancia de la que es modo», cosa que se debe a la «abstracción del espíritu» (Logique, Parte I, cap. V). En general, la abstracción es la posibilidad que tiene nuestro espíritu de «considerar una parte sin considerar la otra, porque estas partes son realmente distintas» (loc. cit.), lo que quiere decir que cuando las partes no son realmente distintas no se ejecuta ninguna abstracción al considerarlas. La noción de abstracción es fundamental en los autores llamados «empiristas», pero hay grandes diferencias entre ellos al respecto. Locke estima que la función de la abstracción es formar ideas generales, las cuales se obtienen cuando se abstrae o separa de las ideas todo lo que determina que una entidad dada sea una existencia particular. Las ideas generales representan más de un individuo: «Las palabras se hacen generales al convertirse en signos de ideas generales» (Essay, III, iii, 6; ésta es la cita de Locke que figura, entre otras del mismo autor, en los Principles de Berkeley, Introducción, 11, y que Berkeley examina críticamente). Las ideas tomadas de existencias particulares «se hacen representantes generales de todas las de la misma clase» (op. cit., II, xi, 9). Hay que tener presente que, para Locke, lo universal y lo general exhibido por las «ideas generales» se halla en éstas y no en las cosas mismas (op. cit., III, iii, 11). A pesar de las cautelas que tomó Locke, Berkeley estimó que había errado, como tantos otros filósofos, al considerar que se pueden fraguar «ideas abstractas» («ideas generales abstractas»). No es posible, afirma Berkeley, representarse cualidades sensibles fuera de la percepción (no se puede representar el movimiento aparte de un cuerpo moviéndose), ni cualidades sensibles generales (el color en general, aparte el rojo, el verde, etcétera), ni el triángulo en general o la triangularidad (aparte de ser rectángulo, obtuso o escaleno), ni el hombre (aparte de ser blanco, negro, alto, bajo, etc.), ni la extensión (aparte de ser línea, superficie, sólido etc.). Pueden usarse legítimamente palabras generales, como en la proposición «el cambio de movimiento es proporcional a la fuerza impresa», pero ello no da pie a mantener la idea de movimiento sin cuerpo que se mueva o sin ninguna determinada dirección o velocidad, pues se limita a indicar únicamente que dicha proposición es verdadera aplicada a cualesquiera cuerpos que se mueven en cualesquiera direcciones (Principles, Int., 11). Por eso Berkeley no se opone a las ideas generales, sino sólo a las ideas generales abstractas, o ideas generales formadas por abstracción (op. cit., 12). Las ideas generales son únicamente ideas particulares que se hacen generales por convertirse en un signo (no un signo de algo abstracto y general, sino de todas las ideas particulares a las cuales la idea general puede aplicarse [loc. cit.]). Sólo adoptando esta actitud, concluye Berkeley, se sale de «los inextricables laberintos de error y disputa» en que se han enzarzado los escolásticos, «esos grandes maestros de la abstracción», por causa de las nociones abstractas (op. cit., 16). Estas conclusiones fueron gratas a Hume, para quien el rechazo de las ideas abstractas por parte de Berkeley es «uno de los mayores y más valiosos descubrimientos de los últimos años» (Treatise, I, vii). Se ha discutido si la crítica de Berkeley a Locke es justa. T. D. Weldon (Kant's Critique of Pure Reason, 2.a ed., 1958, págs. 164 y sigs.) es de opinión que no, ya que Berkeley no parecía tener en cuenta lo que Locke realmente pensaba (aunque expresaba mal) al respecto, esto es, que las ideas generales son «ficciones y estratagemas mentales» (cfr. Essay, IV, vii, 9; véase A PRIORI) y que no es fácil forjarlas, porque —como ocurre con la idea general del triángulo, que no debe ser ni rectángulo ni isósceles ni escaleno, pero que debe ser a la vez todos ellos-, en una idea general «se juntan varias partes de ideas distintas e inconsistentes» (Locke, loc. cit.). En este sentido, una idea general es como el dibujo de un objeto —por ejemplo, un caballo— que puede reconocerse como siendo el dibujo de un caballo sin que se indique si es gordo o flaco, blanco, negro o pardo. Weldon señala que la noción kantiana de esquema (VÉASE) en general es igual a la mencionada noción lockiana de idea general suplementada por la de síntesis, con el fin de evitar la crítica de Berkeley. La noción kantiana de esquema, sin embargo, apunta también Weldon, es más compleja, y posiblemente más fructífera, que la noción lockiana de idea general, porque incorpora la idea de una «regla para formar esquemas». Hamilton relacionó la noción de abstracción con la de atención (Lectures on Metaphysics and Logic; Met. XIII) y puso de relieve que precisión, atención y abstracción «son nombres correlativos del mismo proceso», siendo los dos primeros casi convertibles mutuamente. «Atención y abstracción —escribió Hamilton— son el mismo proceso visto en distintas relaciones. Son, por así decirlo, los polos positivo y negativo del mismo acto» (op. cit.; Logic, VII). Según Dugald Stewart, la abstracción es el «poder que tiene el entendimiento de separar las combinaciones que le son ofrecidas» (Elements, II, iv, 1). En la mayor parte de autores empiristas, la noción de abstracción tiene un sentido primariamente psicológico —o «mental»— y epistemológico —con posibles consecuencias «metafísicas»-, mientras que en otros autores, como muchos escolásticos, tiene un sentido primariamente metafísico, con consecuencias epistemológicas. Fichte estimó que la abstracción permite separar conceptualmente lo que aparece unido en la conciencia. En ésta coinciden la mente y la cosa, pero mediante abstracción cabe separar la mente, como mente en sí, de la cosa, como cosa en sí. Se puede separar asimismo un existente posible (para nosotros) de toda existencia, lo cual no proporciona un concepto de existencia en general, sea positiva o negativa, sino el de fundamento del predicado de existencia en general (Wissenschaftslehre, I, 456, ed. I. H. Fichte). La abstracción permite vaciar «Yo soy» de todo contenido específico y pasar a la proposición lógica fundamental «A = A» —la cual, sin embargo, no es para Fichte deducible de «Yo soy», pues más bien ocurre lo opuesto (op. cit., I, 98-99)-. La abstracción no es mera separación de lo universal a partir de lo particular; en tanto que abstracción absoluta, ejecutada por la razón, permite llegar, o aproximarse, a la pura reflexión de la conciencia de sí misma. Maritain (op. cit. supra y especialmente Sept leçons sur l'être, II, 2) ha tomado a Hegel como blanco muy principal de su crítica de la noción moderna de abstracción; según dicho autor, la idea hegeliana de Ser, con un contenido nulo que la equipara a la idea de Nada, se debe a no haber distinguido entre los aspectos total y formal de la abstracción. El hecho es, sin embargo, que por una parte Hegel entiende 'abstracción' en modos que difieren a veces bastante de usos previos y que, además, son bastante distintos entre sí, aunque formando una especie de «desarrollo». Por ejemplo, en la Fenomenología, Hegel entiende 'abstracción' sobre todo como una actividad mental mediante la cual se lleva a cabo una separación (Trennung) o singularización (Vereinzelung) de un aspecto particular de una totalidad concreta. Se obtiene de este modo un universal vaciado de su particularidad e individualidad. Según Hegel, este tipo de abstracción, propia del entendimiento (Verstand), cercena la realidad —que es concreta, pero también universal— de su riqueza; de ahí el sentido peyorativo que da Hegel a esta forma de abstracción, aun si reconoce su utilidad en la marcha hacia la comprensión «racional» —y «total»— de la realidad. Este sentido de 'abstracción' es «fenomenológico» y no «científico» —en el sentido que da Hegel a estos dos adjetivos-. En este mismo sentido «negativo» y «peyorativo», sin embargo, residen los gérmenes de una noción más «positiva» de la abstracción, pues no sólo los momentos negativos en la dialéctica de la conciencia son «necesarios», sino que también resulta que al negar una «determinación» se «pone» otra. Así, la negación de la abstracción es a la vez «constitutiva». Ahora bien, este acto de «constitución» es posible sólo porque en su marcha dialéctica la conciencia no se detiene en los productos abstraídos -sean el «contenido sensible» o los «meros universales»-, dejándolos subsistir independientemente. Estos «signos negativos» que son las abstracciones, la conciencia los asume y «apropia». Cuando ello tiene lugar, la forma sigue siendo abstracta, pero el contenido es concreto; no se trata, pues, ya de lo «meramente abstracto», sino de lo «abstracto en tanto que se halla en el elemento del pensar». El sentido más «pleno» de 'abstracción' se abre paso en la Fenomenología, pero alcanza su culminación en la Lógica y en la Enciclopedia (especialmente en § 382 de «La filosofía del espíritu»). Se va alcanzando de este modo una noción, o uso, de «abstracción» que es «sistemático» por ser «dialéctico» (y también lo inverso). Lo concreto —lo universal concreto— llega a ser «la verdad de lo abstracto»; lo concreto es «para sí» lo que lo abstracto es meramente «en sí». Lo abstracto sigue siendo «inmediato», «indeterminado» y «unilateral», a diferencia de lo concreto (VÉASE), pero la mediatez, determinación y totalidad están implícitas en él. Lo abstracto es para Hegel puramente negativo sólo cuando queda aislado del movimiento dialéctico. Por eso dice Hegel que lo abstrac-to —en el último sentido indicado— es tal sólo respecto a la forma, pero en sí mismo es algo concreto, siendo la unidad de diversas determinaciones (cfr., entre otros lugares, Vorlesungen über die Geschichte der Philosophie, Einleitung, A 2; Glockner, XVII, 53). En suma: cuando lo abstracto es considerado sólo formalmente no es lo verdadero; su verdad es meramente parcial. Cuando es considerado «filosóficamente» en cambio, por la operación de la razón (Vernunft) y no meramente del entendimiento, «realiza» lo universal en su «concretitud». Entre los autores del siglo XX en quienes las nociones de abstracción y abstracto desempeñan un papel capital, figuran Whitehead y Husserl. Nos referimos al primero en el artículo ABSTRACCIÓN EXTENSIVA. En cuanto a Husserl, ha concebido lo abstracto y lo concreto no en virtud de su separación o no separación de un todo, esto es, en función de su subsistencia o no subsistencia. La teoría husserliana de la abstracción forma parte de una «teoría de las formas puras de los todos y las partes» e incluye, además de la noción de «abstracto», las de «concreto», «pedazo», «momento» y «parte física». Las definiciones fundamentales son: «Llamamos pedazo a toda parte que es independiente relativamente a un todo T. Llamamos momento (parte abstracta) del mismo todo T a toda parte que es no-independiente relativamente a dicho todo»; las «partes abstractas pueden tener pedazos y [los] pedazos pueden tener partes abstractas» (Investigaciones lógicas, III, § 17, trad. Morente-Gaos). «Puesto que una parte abstracta es también abstracta en relación con cualquier todo más amplio y, en general, con cualquier conjunto de objetos que comprenda ese todo, resulta que un abstracto en consideración relativa es eo ipso abstracto en consideración absoluta. Esta última puede definirse como caso límite de la relativa, caso en el cual la relación viene determinada por el conjunto total de los objetos en general; de manera, pues, que no necesita una anterior definición de lo abstracto o no-independiente en sentido absoluto. Según esto, un abstracto puro y simple es un objeto que está en un todo, con respecto al cual es parte no-independiente» (loc. cit.). Esta última caracterización es básica, puesto que pone de manifiesto que la noción de abstracto no está necesariamente correlacionada con la de «universal»; está correlacionada con la de no-independencia en relación a un todo. Varias de las concepciones de lo abstracto y la abstracción reseñadas hasta ahora tienen una dimensión lógica, pero ésta no es la única ni la más importante. El aspecto lógico predomina, en cambio, en autores como Frege, Russell y muchos lógicos y filósofos de la matemática. De ello resultan cambios importantes en la concepción de la abstracción. Uno de ellos es la idea de Frege de que, a diferencia de propiedades extraídas mediante abstracción de objetos singulares, los números cardinales no resultan de abstracciones de este tipo ni, en rigor, de ningún otro tipo, ya que tales números son propiedades de propiedades. Lo que se trata de hacer en este caso es, pues, evitar usar un «principio de abstracción». Según algunos lógicos, la abstracción no se refiere a propiedades comunes a varios entes, sino a clases de objetos relacionados entre sí por alguna propiedad. El punto de partida de la abstracción, que en la lógica clásica era intensional o comprehensivo se hace aquí extensional. En parte de la nueva lógica, el concepto de abstracción está, pues, estrechamente relacionado con la noción de clase. Pero como cada relación (VÉASE) transitiva, simétrica y reflexiva da origen a una clase, resulta que, a diferencia de lo que ocurría en los procesos abstractivos tradicionales, no es necesario atender a una multiplicación creciente de propiedades. Si, por ejemplo, intentamos definir, de acuerdo con Russell, la propiedad abstracta «dirección espacial», la reduciremos previamente a la relación transitiva, simétrica y reflexiva de «paralelismo entre líneas rectas», con lo cual la dirección de una línea es interpretada como la clase de líneas paralelas a esta línea (cfr. Reichenbach, Elements of Symbolic Logic, 1947, § 37). Lo mismo ocurre con la definición abstractiva de la noción de peso. No es ya una propiedad abstracta del cuerpo; el peso de un cuerpo designa más bien la clase de todos los objetos que poseen el mismo peso que el cuerpo en cuestión. Reichenbach señala que ya Leibniz había reparado en que la definición de la igualdad de una propiedad es lógicamente anterior a la definición de tal propiedad. Con ello se intenta responder a la objeción de la lógica tradicional respecto a la prioridad de la entidad que debe ser definida, objeción que va justamente en un sentido inverso al de Leibniz y al de la nueva lógica. En efecto, dice Reichenbach, «un adepto de la lógica tradicional objetaría que con el fin de definir el mismo peso debemos primeramente definir el peso, y luego proceder por la adición de la diferencia específica al género. Pero no hay razón para insistir en este método poco práctico. Es admisible concebir la noción del mismo peso como algo anterior al concepto de peso y definir el último en términos del primero. Esta concepción corresponde al procedimiento efectivo usado en la determinación empírica del peso de un cuerpo. La balanza es un artificio que indica, no el peso, sino la igualdad de peso. Decir que un cuerpo pesa dos libras significa, por lo tanto, lo mismo que decir que el cuerpo tiene el mismo peso que un cierto patrón» (loc. cit.). La «definición por abstracción» se basa en ese procedimiento y en esta inversión de la prioridad tradicional. Para una aclaración sobre el término 'abstracto' tal como es usado en la lógica de las clases y en la lógica de las relaciones véanse CLASE; RELACIÓN. Según Robert Feys (quien se ha basado para ello probablemente en exposiciones de
Alonzo Church) la noción de abstracto en lógica formalizada designa la
operación que da origen a perífrasis abstractas. Unas son de la forma 'xP'
(siendo 'P' una proposición), que Feys llama abstractos proposicionales
(abreviatura de `perífrasis abstractas proposicionales'). Las otras son de la forma
Además de las obras referidas en el texto del artículo, véanse las siguientes. Abstracción en general: H. Schmidkunz Ueber die Abstraktion, 1889.—J. Laporte, Le problème de l'abstraction, 1940. —Giovanni Fausti, Teoria dell'Astrazione, 1947. —R. Bianchi-Bandinelli, Organicità e astrazione, 1956. —Eino Mikkola, Die Abstraktion. Begriff und Struktur. Eine logisch-semantische Untersuchung auf nominalistischer Grundlage mit besonderer Berücksichtigung des Lateinischen, 1964. Abstracción y dialéctica: L. Jordan, Schule der Abstraktion und der Dialektik. Neue Wege begrifflichen Denkens, 1932. —D. Sayer, The Violence of Abstraction: The Analytic Foundations of Historical Materialism, 1987. Abstracción ontológica y metafísica: N. Balthasar, L'abstraction métaphysique et l'analogie des êtres dans l'être, 1935. —D. A. Bonevac, Reduction in the Abstract Sciences, 1982. —E. N. Zalta, Abstract Objects: An Introduction to Axiomatic Metaphysics, 1983. —B. Hale, Abstract Objects, 1988. —K. Campbell, Abstract Particulars, 1990. Abstracción y lógica: E. Jacques, Levels of Abstraction in Logic and Human Action, 1978. —Y. N. Moschovakis, Elementary Induction on Abstract Structures, 1974. —J. J. Katz, Language and other Abstract Objects, 1981. —L. Wright, Better Reasoning: Techniques for Handling Argument, Evidence, and Abstraction, 1982. —M. Furberg, T. Wetterstrom, C. Aberg, eds., Logic and Abstraction: Essays Dedicated to P. Lindstrom on His Fiftieth Birthday, 1986. Definición por abstracción: H. Scholz y H. Schweitzer, Die sogenannte Definition durch Abstraktion. Eine Theorie der Definitionen durch Bildung von Gleichheitsverwandtschaften, 1935. —A. Pikas, Abstraction and Concept Formation, 1965. Abstracción en varios autores y corrientes: P. Gohlke, Die Lehre von der Abstraktion bei Plato und Aristoteles, 1914. —Ulrich Dähnert, Die Erkenntnislehre des Albertus Magnus gemessen an der Stufen der «Abstractio», 1934. —L. M. Habermehl, Die Abstraktionslehre des heiligen Thomas von Aquin, 1933. —A. Rebollo Peña, Abstracto y concreto en la filosofía de Santo Tomás, 1955. — Gustav Siewerth, Die Abstraktion und das Sein nach der Lehre des Thomas von Aquin, 1958. —G. Van Riet, «La théorie thomiste de l'abstraction», Revue philosophique de Louvain, 50 (1952), 853-893. —J. Rohmer, La théorie de l'abstraction dans l'école franciscaine d'Alexandre de Halès à Jean Peckham, 1928. —Mario H. Otero, «La crítica de la abstracción y la teoría del mundo en Berkeley», Cuadernos uruguayos de filosofía, I (1961), 45-103, ed. separada, 1961 (tesis). —Erhard Oeser, Begriff und Systematik der Abstraktion, 1969 (Aristóteles en Santo Tomás, Hegel y Schelling). —Eduard von Hagen, Abstraktion und Konkretion bei Hegel und Kierkegaard, 1969 (tesis). —Julius R. Weinberg, Abstraction, Relation, and Induction: Three Essays in the History of Thought, 1965. —Jules Vuillemin, La logique et le monde sensible: Étude sur les théories contemporaines de l'abstraction, 1971. back to Diccionario de
filosofía | Encyclopedist
|
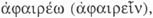 que se traduce por 'abstraer', se usaba comúnmente para
designar el acto de sacar algo de alguna cosa, separar algo de algo, privar a alguien de algo, poner
algo aparte, arrancar algo de alguna cosa, etc. El correspondiente nombre es
que se traduce por 'abstraer', se usaba comúnmente para
designar el acto de sacar algo de alguna cosa, separar algo de algo, privar a alguien de algo, poner
algo aparte, arrancar algo de alguna cosa, etc. El correspondiente nombre es  que se
traduce por 'abstracción' y que significa la acción y efecto de
«sacar», «arrancar», «privar», «separar»,
etc.
que se
traduce por 'abstracción' y que significa la acción y efecto de
«sacar», «arrancar», «privar», «separar»,
etc.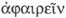 como
como 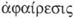 se usaban en muy diversos contextos y con varios significados,
pero éstos se hallan asociados al acto y a la acción y efecto de
«separar», «arrancar», etc. Así,
se usaban en muy diversos contextos y con varios significados,
pero éstos se hallan asociados al acto y a la acción y efecto de
«separar», «arrancar», etc. Así, 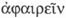 podía
emplearse para designar el acto de declarar que un individuo pasaba a ser un ciudadano, ya que
entonces se lo «arrancaba» o «sacaba» de la esclavitud, o para indicar
la abrogación de un decreto, el cual quedaba entonces «separado del» (o
fuera del) cuerpo legal donde había figurado hasta entonces. El mismo verbo se empleaba
como equivalente a `sustraer' en una operación aritmética y podía usarse
asimismo para designar la acción de suprimir una letra inicial (como en
podía
emplearse para designar el acto de declarar que un individuo pasaba a ser un ciudadano, ya que
entonces se lo «arrancaba» o «sacaba» de la esclavitud, o para indicar
la abrogación de un decreto, el cual quedaba entonces «separado del» (o
fuera del) cuerpo legal donde había figurado hasta entonces. El mismo verbo se empleaba
como equivalente a `sustraer' en una operación aritmética y podía usarse
asimismo para designar la acción de suprimir una letra inicial (como en 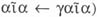 .
. 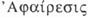 se contrapone a
se contrapone a 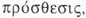 «suma», «colocación de una cosa sobre
otra», añadido de una letra o sílaba (próstasis).
«suma», «colocación de una cosa sobre
otra», añadido de una letra o sílaba (próstasis).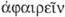 se encuentra en varios pasajes de los escritos de Platón
(Phaed. 67 A, 69 B; Rep. VII, 524 B, 534 B; Parm. 158 C; Pol.
[«El Político»], 280 C; Phil. 26 A; Tim. 35 B), pero no
parece que su uso sea «especializado». De hecho, Platón emplea varios
verbos —
se encuentra en varios pasajes de los escritos de Platón
(Phaed. 67 A, 69 B; Rep. VII, 524 B, 534 B; Parm. 158 C; Pol.
[«El Político»], 280 C; Phil. 26 A; Tim. 35 B), pero no
parece que su uso sea «especializado». De hecho, Platón emplea varios
verbos —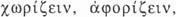
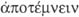 — en sentidos bastante similares, y casi siempre se trata de dar
una idea de algo «separado de algo». Así, por ejemplo, en Rep. VII,
534 B, Platón usa
— en sentidos bastante similares, y casi siempre se trata de dar
una idea de algo «separado de algo». Así, por ejemplo, en Rep. VII,
534 B, Platón usa 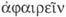 para hablar de la separación del Bien (de la Idea del
Bien) respecto a las demás ideas; en Phaed. 67 C usa
para hablar de la separación del Bien (de la Idea del
Bien) respecto a las demás ideas; en Phaed. 67 C usa 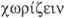 para referirse a la
separación entre el cuerpo y el alma,
para referirse a la
separación entre el cuerpo y el alma, 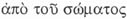
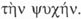 En este último caso tenemos un
uso «corriente» de la noción de «abstracción», esto
es, entendemos lo que traducimos por 'abstracción' como una separación. Ello se
reitera en Phaed. 67 D:
En este último caso tenemos un
uso «corriente» de la noción de «abstracción», esto
es, entendemos lo que traducimos por 'abstracción' como una separación. Ello se
reitera en Phaed. 67 D: 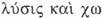
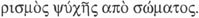 La cuestión es saber si en el primer caso se
entiende la separación como «abstracción» tal como solemos
entenderla hoy, o, mejor dicho, tal como se ha entendido desde Aristóteles en los textos
de muchos filósofos.
La cuestión es saber si en el primer caso se
entiende la separación como «abstracción» tal como solemos
entenderla hoy, o, mejor dicho, tal como se ha entendido desde Aristóteles en los textos
de muchos filósofos.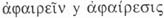 en varios sentidos «corrientes», y que trató de la noción de
«separación» en el significado platónico para someterla a
crítica, elaboró una noción más técnica y especializada de
'abstraer', 'abstracción' y 'abstracto' en varios pasajes, entre los que citamos An.
post. I, 81 b y II, 19, 99 b 17-100 b 17; Met. 1061 a-b; De an. III, 431 b;
De coelo, 299 a 16. No es fácil discriminar entre varios significados de
«abstracción» en Aristóteles, pero en muchos casos este autor se
interesa por un modo de conocer que es el «abstraer», es decir, por un
conocimiento que obtiene, mediante abstracción,
en varios sentidos «corrientes», y que trató de la noción de
«separación» en el significado platónico para someterla a
crítica, elaboró una noción más técnica y especializada de
'abstraer', 'abstracción' y 'abstracto' en varios pasajes, entre los que citamos An.
post. I, 81 b y II, 19, 99 b 17-100 b 17; Met. 1061 a-b; De an. III, 431 b;
De coelo, 299 a 16. No es fácil discriminar entre varios significados de
«abstracción» en Aristóteles, pero en muchos casos este autor se
interesa por un modo de conocer que es el «abstraer», es decir, por un
conocimiento que obtiene, mediante abstracción, 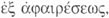 ciertos tipos de objetos o
«realidades». Así, por ejemplo, se obtienen mediante abstracción los
llamados «matemáticos» («objetos matemáticos»);
éstos existen «en la abstracción»,
ciertos tipos de objetos o
«realidades». Así, por ejemplo, se obtienen mediante abstracción los
llamados «matemáticos» («objetos matemáticos»);
éstos existen «en la abstracción», 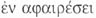 (De an. III 431
b) y no «por sí mismos»,
(De an. III 431
b) y no «por sí mismos», 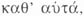 como creen Platón y los
pitagóricos. «Los (objetos) matemáticos» no se hallan
«metafísicamente» separados, esto es, no son, propiamente hablando,
substancias, pero es posible separarlos de la materia mediante conceptos, a diferencia de los
objetos «físicos», que no son separables conceptualmente de la
«materia». He aquí dos tipos o, como se dijo luego, «grados»
de abstracción. El problema es saber si hay otro tipo o «grado» de
abstracción que pueda dar origen a objetos «inteligibles», puras
«formas». Parece que no es posible, a menos de suponer que hay una
«materia inteligible» (cfr. Met. Z, 7, 1036 a), de la que quepa
«abstraer». Si hay tal «materia», entonces tendremos tres formas de
abstracción: matemática, física y «metafísica» o
«inteligible».
como creen Platón y los
pitagóricos. «Los (objetos) matemáticos» no se hallan
«metafísicamente» separados, esto es, no son, propiamente hablando,
substancias, pero es posible separarlos de la materia mediante conceptos, a diferencia de los
objetos «físicos», que no son separables conceptualmente de la
«materia». He aquí dos tipos o, como se dijo luego, «grados»
de abstracción. El problema es saber si hay otro tipo o «grado» de
abstracción que pueda dar origen a objetos «inteligibles», puras
«formas». Parece que no es posible, a menos de suponer que hay una
«materia inteligible» (cfr. Met. Z, 7, 1036 a), de la que quepa
«abstraer». Si hay tal «materia», entonces tendremos tres formas de
abstracción: matemática, física y «metafísica» o
«inteligible».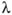 x M' (siendo 'M' una expresión bien formada cualquiera), que Feys llama
abstractos combinatorios (abreviatura de `perífrasis abstractas
combinatorias'). Las primeras aparecen en la lógica usual; las segundas, en la
lógica combinatoria. Aunque sólo implícitamente, estas dos formas se
hallaban ya en Frege. Su análisis muestra que la abstracción puede ser entendida
bajo un aspecto «conceptualista» (único que, siendo propiamente
lógico, corresponde a la «lógica positiva»), pues toda otra
interpretación (realista, nominalista o «conceptualista» en el sentido
tradicional), siendo metalógica, debe ser excluida de la lógica stricto sensu
aun cuando sea considerada filosóficamente legítima. Según ello, se
pueden usar las expresiones 'abstractos proposicionales' y 'abstractos combinatorios' sin
necesidad de una interpretación metalógica.
x M' (siendo 'M' una expresión bien formada cualquiera), que Feys llama
abstractos combinatorios (abreviatura de `perífrasis abstractas
combinatorias'). Las primeras aparecen en la lógica usual; las segundas, en la
lógica combinatoria. Aunque sólo implícitamente, estas dos formas se
hallaban ya en Frege. Su análisis muestra que la abstracción puede ser entendida
bajo un aspecto «conceptualista» (único que, siendo propiamente
lógico, corresponde a la «lógica positiva»), pues toda otra
interpretación (realista, nominalista o «conceptualista» en el sentido
tradicional), siendo metalógica, debe ser excluida de la lógica stricto sensu
aun cuando sea considerada filosóficamente legítima. Según ello, se
pueden usar las expresiones 'abstractos proposicionales' y 'abstractos combinatorios' sin
necesidad de una interpretación metalógica.