CONTINUOCONTINUO.Según Aristóteles, algo
es sucesivo, Ya en la filosofía antigua el problema del continuo (o de lo continuo) fue uno de los problemas filosóficos capitales; en efecto, estaba esencialmente vinculado al problema de la comprensión racional de lo real, y especialmente de «lo lleno» (véase ESPACIO) y por este motivo presentó ya desde los comienzos de la reflexión filosófica algunas graves, aporías (VÉASE). Las más conocidas son las expresadas en las paradojas de Zenón de Elea: la infinita divisibilidad del espacio requiere la anulación del movimiento y de la extensión. Demócrito intentó hallar una solución postulando la existencia de entes indivisibles, donde la racionalidad no penetraba: eran islas irreductibles, rodeadas de discontinuidades y conteniendo en sí mismas, absolutamente compacta y por ello indivisible, una continuidad. La solución de Aristóteles es célebre: consiste en mediar en esta dificultad por medio de las nociones de la potencia y del acto, las cuales solucionan el problema al permitir que un ser pueda ser divisible en potencia e indivisible en acto sin tener que afirmar unívocamente su absoluta divisibilidad o indivisibilidad. Sin embargo, puede decirse que, con excepción de Demócrito y de algunas direcciones «pluralistas», el pensamiento antiguo se inclina casi enteramente hacia la afirmación de lo continuo. Tanto los neoplatónicos como los estoicos coincidían en este punto, aun cuando difirieran en el modo como entendían la continuidad. Los neoplatónicos entendían, en efecto, la continuidad metafísicamente, como algo fundado en la tensión infinita de lo Uno, del cual emanan («continuamente») las demás realidades. Los estoicos entendían la continuidad físicamente: para ellos, el universo es, como lo ha indicado S. Sambursky, «un continuo dinámico», en el cual no hay hiatos o vacíos de ninguna especie, excepto el vacío que rodea a dicho continuo. También se inclinaba en favor de lo continuo el pensamiento medieval, aunque en éste se insertan concepciones que tienden a una especie de discontinuismo de tipo dinámico. Pues en ningún momento puede prescindirse, al atacarse el problema del continuo, de la cuestión de las partes. La definición aristotélica la menciona explícitamente. Lo mismo ocurre en la definición de Santo Tomás, quien señala que es continuo el ente en el cual están contenidas muchas partes en una, y se mantienen simultáneamente. Sin embargo, ya desde antiguo se barruntaba que el problema de lo continuo ofrecía un aspecto distinto según se aplicase a la materia o al espíritu. Y lo que ofrecía, desde luego, dificultad era la continuidad primera, pues debido a la perfecta simplicidad atribuida a lo espiritual, se podía suponer que éste era la extrema concentración de toda continuidad. En el caso de la materia, en cambio, la dificultad subió de punto cuando en la época moderna se replantearon todas las cuestiones de fondo acerca de su constitución. Descartes sostenía una concepción de la materia continua y la identificaba con el espacio. Sin embargo, ello no significaba negar un dinamismo en el fondo de lo material, dinamismo manifestado en la elasticidad. La física cartesiana y la teoría de los «torbellinos» se hallan estrechamente vinculadas con el problema de la continuidad y son uno de los intentos de solucionarlo. Más fundamental todavía es la idea de la continuidad en Leibniz, quien convierte lo que llama el principio de continuidad o también la ley de continuidad en uno de los principios o leyes fundamentales del universo. Esta ley de continuidad exige que «cuando las determinaciones esenciales de un ser se aproximan a las de otro, todas las propiedades del primero deben en consecuencia aproximarse asimismo a las del segundo» (Opuscules et fragments inédits, ed. Couturat, 1903, pág. 108; de una Carta a Varignon, 1702). La ley en cuestión permite comprender que las diferencias que observamos entre dos seres (por ejemplo, entre la semilla y el fruto, o entre diversas formas geométricas, tales como la parábola, la elipse y la hipérbola) son diferencias puramente externas. En efecto, tan pronto como descubrimos clases de seres intermediarias que se introducen entre las dos diferencias, advertimos que podemos ir «llenando» los aparentes vacíos, de tal suerte que llega un momento en que vemos con perfecta claridad que un ser lleva continuamente al otro. Los ejemplos de esta continuidad son, según Leibniz, numerosos: no solamente en las figuras geométricas, sino también en la Naturaleza. Todo está ligado en la realidad de un modo continuo, porque todo está «lleno» (y a la inversa). El principio de continuidad (o ley de continuidad) está perfectamente acordado con el principio de plenitud. Ambos dependen, por lo demás, del principio de razón suficiente. Cuando se niega este último principio se hallan en el universo «hiatos» y discontinuidades. Pero estos «hiatos» y discontinuidades no pueden entonces explicarse, a menos que se haga por medio de milagros o por el puro azar. El principio de continuidad garantiza el orden y la regularidad en la Naturaleza, y es a la vez la expresión de tal orden y regularidad. El poder de la matemática radica en el hecho de que es capaz de expresar la continuidad de la Naturaleza; la Geometría es la ciencia de lo continuo, y «para que haya regularidad y orden en la Naturaleza, lo físico debe estar en constante armonía con lo geométrico» (loc. cit.). Todo está ligado, todo es continuo, todo está «lleno» (cfr. Principes de la nature et de la grâce, § 3; Monadologie, § 54; Nouveau système, § 11 et al.). Pero Leibniz no se limitó a reiterar la idea de continuidad, sino que indicó que puede descubrirse la ley de lo continuo. Del mismo modo que se puede expresar algebraicamente la ley de una curva, por complicada que ésta sea, puede también descubrirse mediante leyes la continuidad en la Naturaleza. Y, en último término, podría descubrirse una ley que sería la ley de la realidad entera y que por el momento solamente podemos expresar señalando su existencia en el principio universal de continuidad. Esta idea no ha sido, sin embargo, aceptada por todos los filósofos; muchos han estimado que parece imposible escapar a las antinomias que Zenón de Elea puso de relieve por vez primera. Así, Kant ha tratado el problema de lo continuo dentro de la segunda antinomia (VÉASE). La tesis afirma la imposibilidad de una divisibilidad infinita, pues de lo contrario el ser se disolvería en una nada. La antítesis sostiene la infinita divisibilidad de una parte dada, pues de lo contrario no habría extensión. Ahora bien, la antinomia se debe según Kant, a que en la tesis el espacio es considerado como algo en sí, y en la antítesis como algo fenoménico. Con ello parece haberse descubierto la raíz de la dificultad. Pero, a la vez, la solución se basa en un supuesto que no es forzoso aceptar ni siquiera es plausible: la división de lo «real» en fenómeno y nóumeno. Suprimido el supuesto, el problema tradicional vuelve a introducirse. En vista de ello, algunos pensadores han considerado o que no tiene solución o que solamente la tiene adoptando —o por convención o por convicción— alguna posición metafísica última. Esta posición puede consistir o en hacer de la continuidad el producto de una yuxtaposición de discontinuidades, o en considerar la discontinuidad como un corte en la continuidad (si se quiere, como un momento de «degradación», de «descenso» de una simplicidad originaria, de tal suerte que espacio y tiempo serán algo «engendrado» por la distensión de un ser absolutamente tenso, continuo e impenetrable). Tales posiciones son —explícita o implícitamente- bastante frecuentes en los metafísicos que han intentado dar una solución al problema; resulta sospechoso, sin embargo, que la primera posición se base en la simple «afirmación» de que hay entidades discretas y en la metáfora de la yuxtaposición, y la segunda se edifique sobre la simple «afirmación» de que hay una —o varias— entidades simples y en la metáfora de la «distensión». Aunque es difícil separar el problema filosófico del continuo de los problemas que plantea la noción de continuidad en la física y en la matemática, nos referiremos ahora más especialmente a esta última noción, que ha sido muy insistentemente dilucidada por físicos y matemáticos durante los últimos siglos. Consideremos ante todo la física. Hay en esta ciencia una noción —la noción de campo— que supone la idea de continuidad pues no se trata de explicar un fenómeno por la acción de partículas, sino por la estructura total de un conjunto físico. Esta noción no es una novedad en la física contemporánea. Estaba ya latente en la llamada física clásica a partir del siglo XVII a consecuencia de la tesis de la «acción a distancia». Pero como constituía una especie de «cuerpo extraño» dentro de la física y, además, algo inexplicable, se consideró que llegaría un día en que podría ser arrumbada. No ocurrió así. Por el contrario, la teoría electromagnética de Maxwell precisó la noción de referencia en la cual se insertaron luego las concepciones relativas a las radiaciones, que aparecieron como perturbaciones del campo electromagnético. Tales concepciones chocaron con el discontinuismo atomista. Se reprodujeron así, pero agudizadas, cuestiones que se habían planteado anteriormente en el problema de la naturaleza -ondulatoria o corpuscular— de la luz. En vista de ello las concepciones continuistas y discontinuistas chocaron entre sí con gran frecuencia. Durante algunos instantes pareció triunfar el continuismo: las físicas cualitativistas y continuistas de Mach, Ostwald y (en parte) Duhem realizaron en este sentido un gran esfuerzo. Luego —sobre todo con la teoría de los cuantos— pareció imponerse el discontinuismo. Y buena parte del trabajo en la física durante los últimos treinta años puede ser estudiado desde el punto de vista de la oposición —y esfuerzos de conciliación— de las dos concepciones. Así, por ejemplo, la mecánica ondulatoria mostró la posibilidad de unir las nociones de campo y de partícula en la noción de la onda-corpúsculo (partícula a la cual está asociado un campo ondulatorio). Esto no significa, ciertamente, que haya diferencias entre la onda y el corpúsculo; de hecho ocurre sólo que cada uno obedece a una estadística diferente (las ondas, a la estadística Bose-Einstein; los corpúsculos elementales, a la estadística Fermi-Dirac). Se dirá que las mencionadas nociones tienen poco que ver con lo que los filósofos entienden por continuidad y discontinuidad y, por consiguiente, que no es legítimo trasplantar a los físicos las preocupaciones que solamente son propias de los filósofos. Sin embargo, no es éste el caso. Aunque los físicos están poco inclinados a plantear tales problemas en los mismos términos usados por los filósofos y se resisten a una interpretación precipitada de los resultados de su ciencia, lo cierto es que buscan ciertas soluciones que pueden inscribirse en la cuenta de alguna de las concepciones mencionadas o en la síntesis de ellas. Podemos mencionar a este respecto la proposición de Heisenberg de una «longitud mínima», de la cual todas las longitudes serían múltiplos, lo que equivaldría a reconocer la posibilidad de «dividir» la longitud en cantidades discretas. Podemos señalar, asimismo, el hecho de que Louis de Broglie ha insistido en que no sólo todo fenómeno macroscópico observable corresponde a un número enorme de transiciones cuánticas elementales, sino que esto muestra hasta qué punto las dificultades y antinomias suscitadas por el problema de la divisibilidad infinita de un segmento de espacio o de tiempo y, de consiguiente, toda la cuestión del «laberinto del continuo» se desvanece o atenúa en la escala microfísica. (Observemos, empero, que L. de Broglie propuso en 1956 la teoría según la cual corpúsculos y cuantos de energía pueden ser considerados como deformaciones ondulatorias de un campo único: el espacio.) Es cierto que la última fórmula einsteiniana (que no es todavía susceptible de comprobación física) para la unificación de la luz, el magnetismo, la radiación y la gravitación en un «continuo» puede poner en tela de juicio la entera teoría de los cuantos (a causa del carácter no discreto de la gravitación). Pero no hace mucho tiempo que J. Schwinger presentó un sistema de ecuaciones del cual parece poder deducirse la «existencia» de «partículas mínimas de espacio-tiempo» de las cuales todos los «segmentos espacio-temporales» serían múltiplos. En suma, aunque el físico, y en ocasiones el filósofo, se resistan a interpretaciones demasiado intuitivas y, por ende, peligrosas de las teorías de la física (VÉASE), y se afirme que, en ausencia de una representación intuitiva, no se puede decir que haya un giro hacia el continuismo o hacia el discontinuismo en dicha ciencia, no se puede evitar dar una interpretación a ciertas soluciones. Y aun si adoptamos para el presente problema el principio de complementaridad (VÉASE) y hacemos de la continuidad y de la discontinuidad algo así como «conceptos-límites», estos conceptos siguen operando si se quiere que posean alguna significación y, por lo tanto, no son enteramente eliminables. El problema de la continuidad en matemáticas se planteó con las antinomias o paradojas de Zenón de Elea. Proclo consideró que un número dado es como un «corte» en la «compacta espesura» del continuo de los números reales. El «corte» en tal continuo es comparable al «corte» de una línea por otra. Las dificultades que plantea dilucidar la noción de continuo en matemáticas llevaron a Leibniz a hablar del «laberinto del continuo». Sin embargo, ha sido frecuente hablar de la matemática —especialmente al considerarse la serie de números reales o los puntos en una línea— como «el reino de lo continuo». La vaga idea filosófico-matemática de continuidad experimentó, según ciertos autores, un vuelco cuando Weierstrass descubrió la existencia de funciones discontinuas y de funciones continuas sin derivadas. La noción de continuo se ha usado en matemáticas especialmente dentro de la teoría de los conjuntos cantorianos, cuando se ha planteado el llamado «problema del continuo». Tratamos del mismo en el artículo CONTINUO (HIPÓTESIS DEL). La noción de continuo en varios autores: G. Schilling, Aristotelis de continuo doctrina, 1840 (tesis). —Aldo Masullo, La problematica del continuo nel pensiero di Zenone di Elea e di Aristotele, 1955. —Maurice Clavelin, «Le problème du continu et les paradoxes de l'infini chez Galilée», Thalès (1959), 1-26. —D. Furley, J. Murdoch et al., Infinity and Continuity in Ancient and Medieval Thought, 1982, ed. N. Kretzmann. —R. Sorabji, Time, Creation, and the Continuum: Theories in Antiquity and the Early Middle Ages, 1983. La noción de continuidad, en matemáticas y en física, ha sido tratada en: L. Couturat, «Sur la définition du continu», Revue de Métaphysique et de Morale, 8 (1900), 157-158. —E. V. Huntington, «The Continuum as a Type of Order», Ann. of Mathematics (1905). —E. B. Wilson, «Logic and the Continuum», American Mathematical Society Bulletin, 14 (1908). —Hermann Weyl, Das Kontinuum. Kritische Untersuchungen über die Grundlagen der Analysis, 1918, reimp. en el vol. Das Kontinuum, 1962, con otros trabajos de F. Landau, B. Riemann et al. —Íd., íd., Philosophie der Mathematik und Naturwissenschaft, 1927 (trad. ingl., ampliada por el autor: Philosophy of Mathematics and Natural Science, 1959). —Varios autores, «Concepts of Continuity», Proceedings of the Aristotelian Society, Supl. vol. 6 (1924). —H. Buchholz, «Das Problem der Kontinuität. Die Unmöglichkeit absoluter metrischer Präzision», Grundfragen der Philosophie, Heft 1, 1927. —F. Warrain, Quantité, infini, continu, 1928. —L. de Broglie, Continu et discontinu, 1941. —Jean Cavaillès, Transfini et continu, 1947. —R. Carnap, The Continuum of Inductive Methods, 1952. —J. E. Murdoch, E. A. Synan, «Two Questions on the Continuum», Franciscan Studies, 26 (1966). —F. Brentano, Philosophische Untersuchungen zu Raum, Zeit und Kontinuum, 1976. Para el «problema del continuo», véase bibliografía en CONTINUO (HIPÓTESIS DEL). back to Diccionario de filosofía | Encyclopedist
|
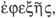 de algo cuando se halla después de él en algún
respecto sin que haya nada más en medio de la misma clase (Phys., V 3, 226 b
34-227 a 1). Cuando se trata de cosas, el hecho de estar una sucediendo a la otra produce la
contigüidad, el ser contiguo,
de algo cuando se halla después de él en algún
respecto sin que haya nada más en medio de la misma clase (Phys., V 3, 226 b
34-227 a 1). Cuando se trata de cosas, el hecho de estar una sucediendo a la otra produce la
contigüidad, el ser contiguo, 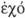
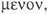 o contacto. Dos cosas están en contacto
cuando sus límites exteriores coinciden en el mismo lugar. Cuando hay contacto, hay
contigüidad, pero no a la inversa (como sucede con los números, que son
contiguos, pero no se hallan en contacto). La contigüidad es una especie de la que la
continuidad es un género. «Los extremos de cosas pueden estar juntos sin
necesariamente ser uno, pero no pueden ser uno sin estar necesariamente juntos»
(ibid., 227 a 22-24). Dos cosas son continuas cuando sus límites son
idénticos,
o contacto. Dos cosas están en contacto
cuando sus límites exteriores coinciden en el mismo lugar. Cuando hay contacto, hay
contigüidad, pero no a la inversa (como sucede con los números, que son
contiguos, pero no se hallan en contacto). La contigüidad es una especie de la que la
continuidad es un género. «Los extremos de cosas pueden estar juntos sin
necesariamente ser uno, pero no pueden ser uno sin estar necesariamente juntos»
(ibid., 227 a 22-24). Dos cosas son continuas cuando sus límites son
idénticos, 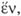 a diferencia de dos cosas contiguas, cuyos límites
están juntos. En otro lugar (Met.,
a diferencia de dos cosas contiguas, cuyos límites
están juntos. En otro lugar (Met., 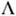 1069 a 1-2) Aristóteles define lo
continuo,
1069 a 1-2) Aristóteles define lo
continuo, 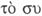
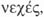 como aquella magnitud cuyas partes están unidas en un todo por
límites comunes. Aristóteles distingue entre varios conceptos: el ser sucesivo,
como aquella magnitud cuyas partes están unidas en un todo por
límites comunes. Aristóteles distingue entre varios conceptos: el ser sucesivo,
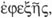 el ser continuo,
el ser continuo, 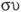
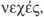 el ser contiguo,
el ser contiguo, 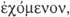 el hecho de tocarse,
el hecho de tocarse, 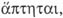 pero al
mismo tiempo intenta examinar qué relaciones existen entre tales conceptos. Muchos
escolásticos que se inspiraron en Aristóteles, y en particular Santo Tomás,
estudiaron asimismo estos conceptos con la intención de analizar su significado y los
diversos modos de su significado (así, por ejemplo, al estudiar el concepto de contacto,
contactus, Santo Tomás lo divide en corporal o corpóreo y espiritual, en
contacto cuantitativo y contacto virtual, etc.). Analizar la historia de todos y cada uno de estos
conceptos sería tarea larga. Además, uno de estos conceptos —el de contacto— ha
experimentado numerosas vicisitudes en el curso de la época moderna, cuando
científicos y filósofos se ocuparon del problema de cómo es posible, o de
si es posible, la producción de efectos en los cuerpos sin contacto, del problema de si
puede concebirse una «acción a distancia». Nos limitaremos a bosquejar una
historia de lo que podría llamarse el debate entre los «continuistas» y los
«discontinuistas», es decir, entre quienes consideran que la realidad —la realidad
física primariamente pero también toda realidad como tal— es continua o
discontinua. En el curso de este debate se han dado, además, numerosas opiniones sobre
la naturaleza de la continuidad.
pero al
mismo tiempo intenta examinar qué relaciones existen entre tales conceptos. Muchos
escolásticos que se inspiraron en Aristóteles, y en particular Santo Tomás,
estudiaron asimismo estos conceptos con la intención de analizar su significado y los
diversos modos de su significado (así, por ejemplo, al estudiar el concepto de contacto,
contactus, Santo Tomás lo divide en corporal o corpóreo y espiritual, en
contacto cuantitativo y contacto virtual, etc.). Analizar la historia de todos y cada uno de estos
conceptos sería tarea larga. Además, uno de estos conceptos —el de contacto— ha
experimentado numerosas vicisitudes en el curso de la época moderna, cuando
científicos y filósofos se ocuparon del problema de cómo es posible, o de
si es posible, la producción de efectos en los cuerpos sin contacto, del problema de si
puede concebirse una «acción a distancia». Nos limitaremos a bosquejar una
historia de lo que podría llamarse el debate entre los «continuistas» y los
«discontinuistas», es decir, entre quienes consideran que la realidad —la realidad
física primariamente pero también toda realidad como tal— es continua o
discontinua. En el curso de este debate se han dado, además, numerosas opiniones sobre
la naturaleza de la continuidad.